Schalal

Lecture #5：Advanced Statistical Models

回归模型的交互项（Interaction）

Interaction: An interaction occurs when an independent variable has a different effect on the outcome depending on the values of another independent variable.

变量之间存在交互效应（Interaction Effect）/协同效应（1+1>2, Synergic Effect）/调节效应（Moderation Effect）时，可以考虑在模型中引入交互项，形式表达上就是两个变量相乘，以两个自变量\(X\)和\(Q\)为例，考虑交互项后线性回归可以写为：

\[Y=\beta_0+\beta_1X+\beta_2Q+\beta_3XQ+\epsilon\]

交互项的意义在于可以直接通过回归系数对\(Q\)与（\(X\)和\(Y\)）关系的影响（反之同理）做一判断。

举例来说，假设\(Y\)是VMT，\(X\)是收入，\(Q\)是0-1变量，标识居住区位（0-乡村，1-城市），当不考虑居住区位和收入的交互效应时，模型即为：\(Y=\beta_0+\beta_1X+\beta_2Q+\epsilon\)，此时不论居住区位，X对Y的影响均为\(\beta_1\)（收入每增加1个单位，VMT增加\(\beta_1\)个单位）；考虑交互效应后，按上述建立回归模型，令\(Q=0\)，即固定居住区位为乡村时，收入对VMT的影响为\(\beta_1\)，令\(Q=1\)，即固定居住区位为城市时，收入对VMT的影响变为\(\beta_1+\beta_3\)，则可以说\(\beta_3\)是居住区位对收入和VMT关系的影响大小，可以衡量居住在城市比居住在乡村时收入对VMT影响的差异。同理，如果固定收入水平不变，可以得到居住在城市比居住在乡村对VMT的影响差异为\(\Delta Y=\beta_2+\beta_3X\)，可以将\(\beta_3\)视作收入水平的变化带来的居住区位对VMT影响的差异。

如果在回归模型中引入了交互项后出现了多重共线性，而不是变量本身的共线引起的共线性，可以考虑以下方法处理：

• 重新评估交互项的必要性：确认交互项是否真正对模型有重要影响。有时候，引入交互项可能并不是必要的，可以重新评估模型的需求和目标，并考虑是否需要保留交互项。

• 重新定义交互项：如果存在共线性问题，可以重新定义交互项，使用其他变量的组合或加权组合代替原始的交互项。这样可以减少变量之间的相关性，从而降低多重共线性的影响。

• 其他一般处理方法：使用正则化方法、增加样本量、PCA等。

分层回归（Hierarchical Linear Model）

参考：https://zhuanlan.zhihu.com/p/150878441，https://andrewwang.rbind.io/courses/bayesian_statistics/notes/Ch10_h.pdf

统计中，内部一致性高于外部一致性的集合可以被称为一个聚类(cluster)。而包含聚类的数据集，就是嵌套数据集(nested data)。

几种分析嵌套数据集的方式：

• 使用一般线性模型：聚类内每一个观测的误差之间存在相关->有效样本量被高估，假阳性概率增加；同时也无法分析不同层级（如群体水平和个体水平）变量之间的关系。
• 先取同一聚类的平均数，再进行一般线性回归：消除了样本之间的观测存在相关性的影响，但是连带个体差异也消除了，只是对群体特征进行了回归。
• 使用多层线性回归：在不浪费样本，可以研究个体差异的同时，也确保了误差独立假设不被违背；但同时需要估计的参数数量增加，需要更多的样本量。

假设有\(j\)个学校，每个学校有\(i\)个学生样本，\(y_{ij}\)表示该学生样本的成绩，\(x_1\)表示学生的家庭状况，则HLM的一般形式：

\[{\text{Level 1:}} \qquad y_{ij} = \beta_{0j}+\beta_{1j} x_{1ij} + \epsilon_{ij}\\ {\text{Level 2:}} \qquad \beta_{0j}=\gamma_{00}+u_{0j}+\delta_{0j}\\ \qquad \qquad \beta_{1j}=\gamma_{10}+u_{1j}+\delta_{1j}\\ \epsilon_{ij} \sim N(0,\sigma_y^2)\\ \begin{pmatrix}\delta_{0j} \\ \delta_{1j}\end{pmatrix} \sim N( \begin{pmatrix}0\\0\end{pmatrix},\begin{pmatrix}\sigma_{\beta_0}^2 \quad , \rho\sigma_{\beta_0}\sigma_{\beta_1}\\ \rho\sigma_{\beta_0}\sigma_{\beta_1}, \quad \sigma_{\beta_1}^2\end{pmatrix})\]

如果直接以一般的线性模型进行建模，则为：\(Y=\beta_0+\beta_1 X+\epsilon\)，可以发现Level 1的HLM与一般的线性模型形式上完全一致，区别在于Level 2，可以做如下解读：

• \(\gamma_{00}\)表示的是固定截距，指在所有学校中截距共有的部分，即样本平均截距。而\(u_{0j}\)表示的就是学校 j 的截距与平均截距的误差。比如，学校1的截距就是\(\gamma_{00}+u_{01}\)；
• \(\gamma_{10}\)表示的是固定斜率，指在所有学校中斜率共有的部分，即样本平均斜率。而\(u_{1j}\)表示的就是学校 j 的斜率与平均斜率的误差。比如，学校1的的斜率就是\(\gamma_{10}+u_{11}\)。

由此引出HML中两种效应的定义：

• 固定效应（fixed effects）：在第二水平上不变的效应
• 随机效应（random effects）：在第二水平上变化的效应
• 混合效应模型（mixed effects）：同时包括随机效应和固定效应

多层模型完全包含了随机效应、固定效应和混合效应模型，上述模型中\(\sigma_y^2\)为组内方差，\(\sigma_{\beta_0}^2,\sigma_{\beta_1}^2\)为组间方差，以\(\sigma_{\alpha}^2\)表示组内方差，组内相关系数 (intraclass correlation coefficient, ICC)定义为：

\(ICC=\frac{\sigma_{\alpha}^2}{\sigma_{y}^2+\sigma_{\alpha}^2}\) Sagan (2013) 建议 ICC 小至 0.05~0.20 之间都应当采用分层模型。

此外，如果第二层中也考虑预测变量，此时称之为完整模型，则HLM将写为：

\[{\text{Level 1:}} \qquad y_{ij} = \beta_{0j}+\beta_{1j} x_{1ij} + \epsilon_{ij}\\ {\text{Level 2:}} \qquad \beta_{0j}=\gamma_{00}+\gamma_{01}w_{0j}+u_{0j}+\delta_{0j}\\ \qquad \qquad \beta_{1j}=\gamma_{10}+\gamma_{11}w_{1j}+u_{1j}+\delta_{1j}\]

三层及以上模型也类似。

可以直接使用statsmodel的mixedlm()函数进行模型的构建与求解，可以参考：https://www.statsmodels.org/dev/mixed_linear.html https://www.statsmodels.org/dev/examples/notebooks/generated/mixed_lm_example.html

结构方程模型（Structural Equation Model）

参考：https://kevintshoemaker.github.io/NRES-746/SEM.RMarkdown.html 《空间数据分析》

路径图与路径分析：在遗传学中，很多现象具有明显的因果关系，如父代与子代的基因关系，父代在前，子代在后，二者的关系只能是单向的，而非对称的。对这种变量结构进行思考，遗传学家Sewall Wright于1918-1921年提出路径分析（path analysis），用来分析变量间的因果关系。

路径分析的主要工具是路径图，它采用一条带箭头的线（单箭头表示变量间的因果关系，双箭头表示变量间的相关关系）表示变量间预先设定的关系，箭头表明变量间的关系是线性的，很明显，箭头表示着一种因果关系发生的方向。在路径图中，观测变量一般写在矩形框内，不可观测变量一般写在椭圆框内。

以下是使用路径分析的基本假设：

1. All relations are linear and additive. The causal assumptions (what causes what) are shown in the path diagram.
2. The residuals (error terms) are uncorrelated with the variables in the model and with each other.
3. The causal flow is one-way.
4. The variables are measured on interval scales or better.
5. The variables are measured without error (perfect reliability).

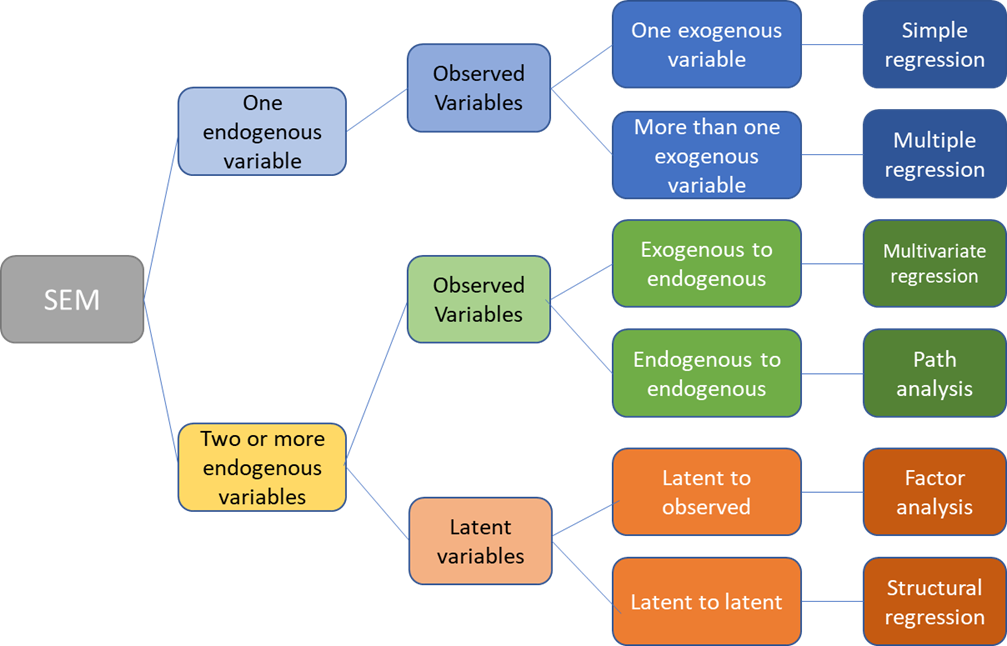
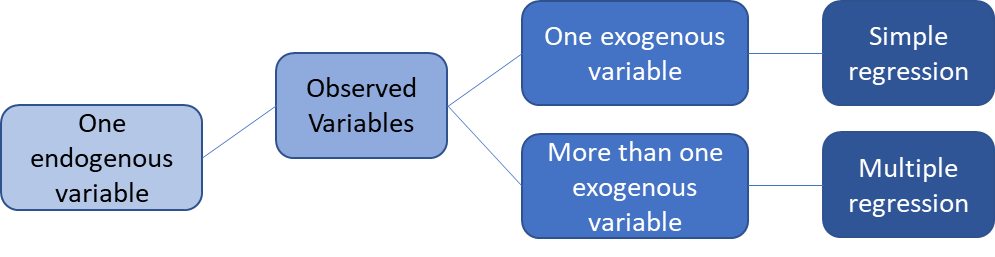
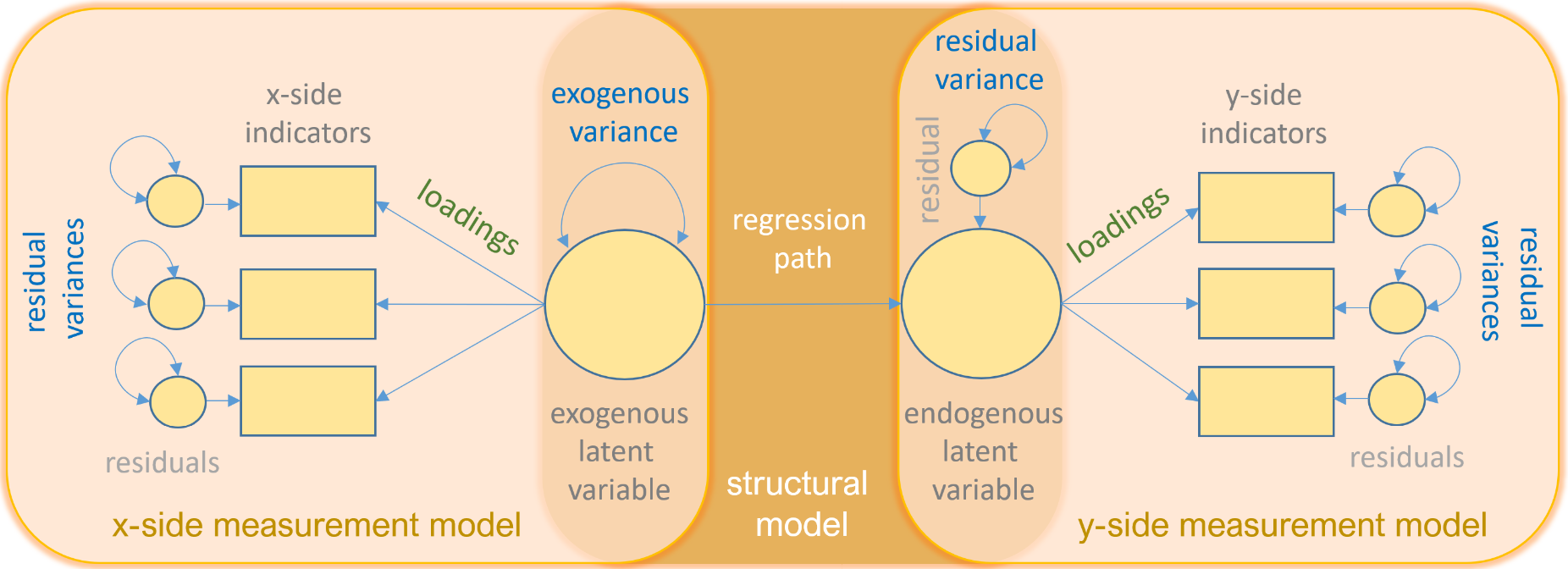
结构方程模型是一种建立、估计和检验因果关系模型的方法，由测量模型和结构模型两部分组成，传统的路径分析类似于SEM中的结构模型部分，但路径分析使用的是观测变量而SEM使用的是潜在变量（？）。

结构方程模型的几类变量的名词解释：

• Observed variable（测量变量，也称为显变量） - Exists in data，在实验中可以直接测量的变量
• Latent variable（潜在变量，也称为隐变量） - Constructed in model，无法被直接观测或测量，可以在模型中通过涉及的若干测量变量加以反映或衡量
• Exogenous（外生变量） - Independent that explains endogenous (observed or latent) (predictor)，只起解释变量作用的变量，在模型中只影响其他变量而不受其他变量影响，不产生测量误差
• Endogenous（内生变量） - Dependent that has a causal path leading to it (observed or latent) (response)，受其他变量影响的变量，可以产生误差项
• Measurement model（测量模型） - Links observed and latent variables，使用测量变量构造潜在变量的模型
• Indicator（指标） - Observed (exogenous or endogenous)，测量变量均为指标，无论是内生的还是外生的
• Factor（因子） - Latent (exogenous or endogenous)，潜在变量均为因子，无论是内生的还是外生的
• Loading - Path between indicator and factor
• Structural model - specifies causal relationships between exogenous and endogenous variables，反映潜在变量和潜在变量之间的关系（无论内生或外生）
• Regression model - Path between exogenous and endogenous variables

一些关于上述名词的示意图：

整体来看，结构方程模型的构建步骤:

1. 模型建构（model specification），指定观测变量与潜变量（因子）的关系、各潜变量间的相互关系（指定哪些因子间有相关或直接效应），在复杂的模型中，可以限制因子负荷或因子相关系数等参数的数值或关系；
2. 模型拟合(model fitting)，主要的是模型参数的估计(ML或GLS等)；
3. 模型评价（model assessment），结构方程的解是否适当( proper)，估计是否收敛，各参数估计值是否在合理范围内（例如，相关系数在 +1与－1之内）；参数与预设模型的关系是否合理；当然数据分析可能出现一些预期以外的结果，但各参数绝不应出现一些互相矛盾，与先验假设有严重冲突的现象；A model is considered a good fit if the value of the chi-square test is insignificant, and at least one incremental fit index (like CFI, GFI, TLI, AGFI, etc.) and one badness of fit index (like RMR, RMSEA, SRMR, etc.) meet the predetermined criteria. 大样本情况下的理想情况：NFI,NNFI,CFI,IFI,GFI,AGFI,RFI大于0.9，RMR小于0.035，RMSEA小于0.08
4. 模型修正（model modification）(1)如模型评价结果中含有没有实际意义或统计学意义的参数时，可以将这些参数固定为零，即删除相应的自由参数；(2)如模型的某个或某几个固定参数的修正指数（MI）比较大时，原则上每次只将那个最大或较大MI的参数改为自由参数。理由是：假设某一固定路径的MI原本很大，需要自由估计，但当修改其他路径后，这MI可能已变小，对应的路径无需再改动。因此，每次只修改一个固定路径，然后重新计算所有固定路径的MI。但MI受样本容量的影响，因此，不能把MI的数值作为修改的唯一根据 。(3)当评价结果中有较大的标准残差时，分两种情况：一是当有较大的正标准残差时，需要在模型中添加与残差对应的一个自由参数；二是当有较大的负标准残差时，则需要在模型中删除与残差对应的一个自由参数。通过不断添加与删除自由参数，直到所有的标准残差均小于2为止。(4)如果主要方程的决定系数很小，则可能是以下某个或某几个方面的原因：一是缺少重要的观察变量，二是样本量不够大，三是所设定的初始模型不正确。

可以借助Python的semopy库进行SEM的构建，semopy stands for Structural Equation Models Optimization in Python and is designed to help statisticians that employ SEM techniques to handle their research in a more Pythonic way. We want to fill a niche of SEM tools in Python that is seemed to be empty as we found ourselves and several other researchers to be unsatisfied using either commercial software or dealing with older computer languages.

Quick Start: https://gitlab.com/georgy.m/semopy/-/blob/master/notebooks/semopy%20-%20Walkthrough.ipynb

This site is open source. Improve this page.